The mushroom data set is a nominal (not ordered, not quantitative) table with 8124 rows and 23 columns. Class, with the 2 values edible and poisonous, is one column. The number of edible mushrooms is 4208 and the number of poisonous ones is 3916. Other attributes have different numbers of values. Habitat, for example, has 7, namely urban, grasses, woods, paths, waste, and meadows. In the original data file the values were coded as letters, but this was translated back into the names from the legend for readability. Here is a screen shot of the Open Office Calc spreadsheet.
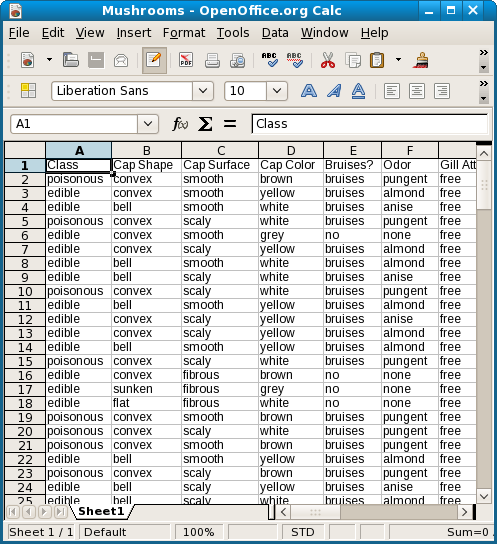
This .csv file of the data table was then imported into a SQLite database. SQLite is a widely used embedded data base which supports the System Query Language. SQL is the standard for relational database access. All analyses and tests on the database were performed with Sqliteman, a freely availble GUI tool for SQLite. Sometimes the .csv file itself was also tested, using the AutoFilter function, which is part of Open Office Calc. For more complicated queries, however, SQL and SQLite were preferred.
Executing a reduction with Emping-0.6 with Class as consequent attribute took 6 minutes, i.e. 3 minutes for each of the 2 attribute values. The reduction resulted in 3635 rows of different rules, each uniquely determining edible or poisonous. There are 1980 rules for poisonous and 1655 for edible.

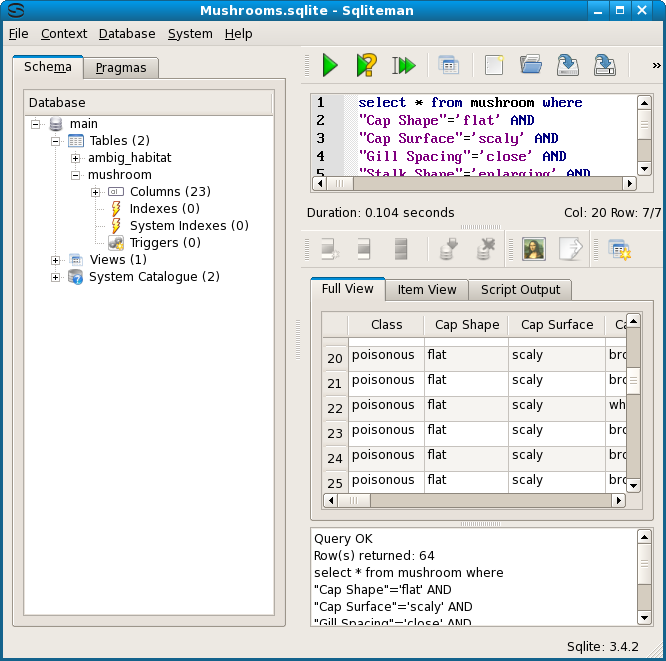
The reduced rules are ordered by length by Emping, so the last one for each predicate is the longest, or equal to another longest. Rule number 1980 (line number 1981) with six predicates was tested in the database and resulted in 64 rows, all poisonous as expected. Here's the screen shot.
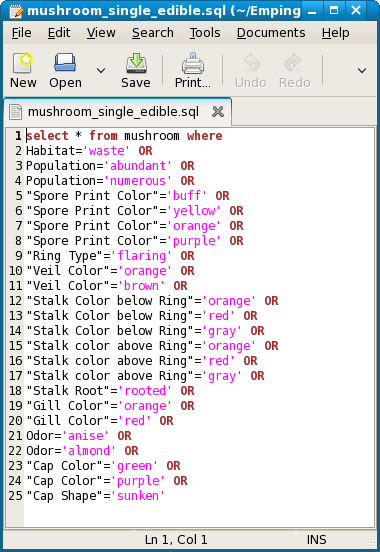
Because of the ordering by length it is easy to find all singleton predictors. The following query resulted in 3897 rows, all poisonous, as expected.

For those unfamiliar with SQL, the meaning follows intuition. All rows (wildcard *) are those which have the stated column attribute values, selected from the specified table, This particular query was built up sequentially, with each additionol OR sperately tested for its result. As expected, each added one or more rows of poisonous mushrooms. A similar query was done for edible, with 2752 rows as result.
Of course these can be combined to give all rows, either edible or poisonous, which can be predicted by a single attribute value. This resulted in 6649 rows, which adds up with the results from the separate queries.
These results, which were obtained from the database, were independently checked in the OO Calc spreadsheet using the filtering feature.
The number of columns which contained all 45 predicates was 14. For the Class attribute 82 % of all rows can be predicted from single attribute values in 64% of the columns.
Discovery of the singletons, of course, could easily have been accomplished by testing each of the 119 attribute values. The value of Emping comes from the identification of all possible combinations, and of their possible relations.
This process is called abduction and it took less than a minute for both poisonous and edible. The results were, 942 equivalence classes for poisonous, and 950 for edible. Of these poisonous has 61 most general rule groups, and edible has 109. The graphs in .dot (Graphviz) format, as rendered by dotty, showed a mass of entailment relations between these groups of equals, with no clear pattern. The following are two screen shots of the most general rule equivalences for edible. Each picture shows the same rules, the first taken from the left, and the second from the right. The number in the leftmost column is the node number in the .dot graph. Then comes each equivalence class, as shown in the second screen shot. As can be seen, some rules have no equivalencent representations, others have several. For readability, each equivalent group is separated by a blank line.

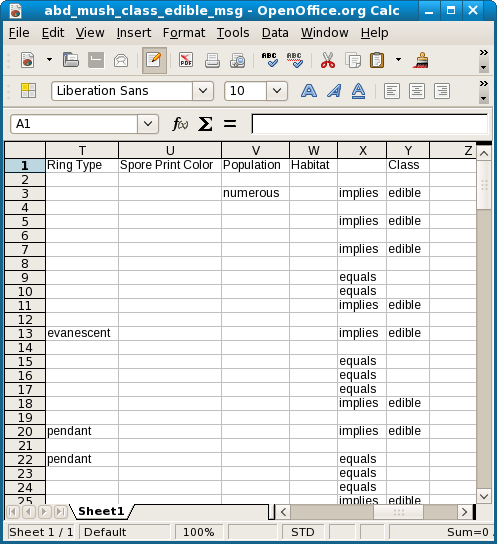
It can be shown that an odor of anise or almond, or a population of numerous, not only imply an edible mushroom, but that there is no more general characterization. These predictors are also in the least general set of rules, which means these stand alone. They neither imply, nor are implied, by any other rules.
This is different for Habitat= abundant. Though all 384 of these cases are edible, they also have a broad Gill Type and an evanescent Ring Type.
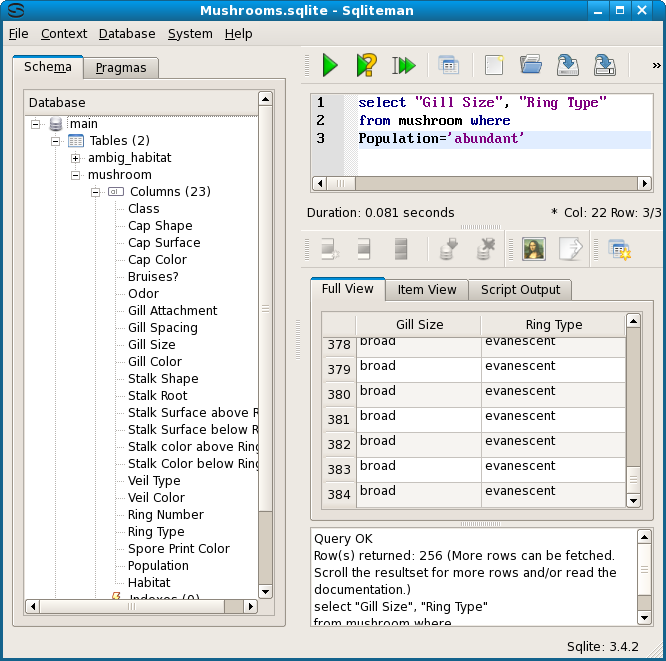
But this matches node 49 in the abduction graph, as indicated by the most general (and the abduction for edible) spreadsheet files. So, the number of rows with broad Gill Type and evanescent Ring Type must be larger than the number for Habitat= abundant. Indeed, it turns out there are 960, and, as Emping had found, all edible. Actually, all such entailments are traceable through the .dot graphs, but because of the size and complexity of these for Class this is not very practical. But look at example 3.